Image processing

Overview

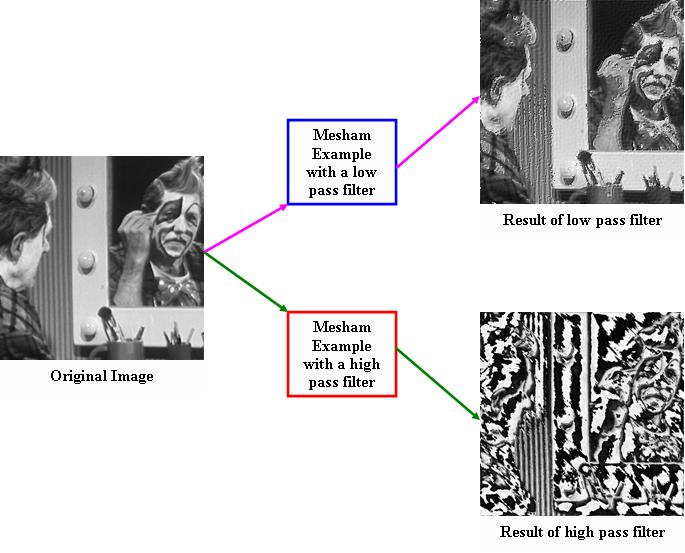
This example is one of the more complex examples we have written in the language. It allows the user to perform some parallel image processing on a black and white image. The image processing supported is applying a low or high pass filter on the image. However, to do this the image needs to be transformed into the frequency domain - and then requires transformation back into the time domain. At the core of the example is the FFT kernel, this is a basic Cooley Turkey FFT algorithm and there are more efficient ones out there. Having said that, the type information provided by the programmer allows the compiler to perform a large amount of optimisation during the translation process. By playing around you can change the filters and also invoke the high pass filter rather than the lowpass which the code does at the moment.

Performance

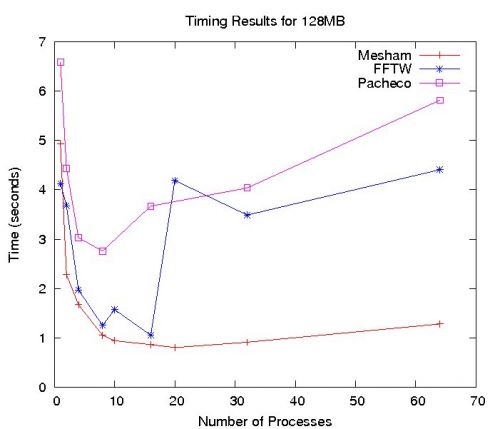
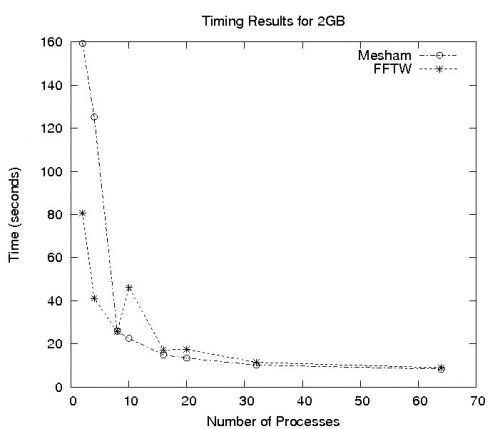
Performance of the Fast Fourier Transform (FFT) has been evaluated on a super computer cluster. Two different experiments were performed, one with an image size of 128MB and the other with an image size of 2GB. Evaluations were performed against the Fastest Fourier Transformation in the West (FFTW) and a book example for 128MB. As can be seen with an uneven distribution of data (10 and 20 processors) FFTW experiences severe slowdowns whereas the Mesham version does not (the compiler will optimise the code in this case to avoid any slow down.)

Source Code

#include <maths>
#include <io>
#include <string>

var n:=256; // image size
var m:=4; // number of processors
var filterThreshold:=10; // filtering threshold for high and low pass filters

function void main() {
   var a:array[complex,n,n] :: allocated[single[on[0]]];
   var s:array[complex,n,n] :: allocated[horizontal[m] :: single[evendist]];
   var s2:array[complex,n,n] :: allocated[horizontal[m] :: col[] :: single[evendist]];
   var s3:array[complex,n,n] :: allocated[horizontal[m] :: single[evendist] :: share[s2]];
   proc 0 {
      loadfile("data/clown.ppm",a);
      moveorigin(a);
   };
   s:=a;
   var sinusiods:=computesin();
   var p;
   par p from 0 to m - 1 {
      var i;
      for i from s[p].low to s[p].high {
         FFT(s[p][i-s[p].low],sinusiods);
      };
   };
   s2:=s;
   par p from 0 to m - 1 {
      var i;
      for i from s[p].low to s[p].high {
         FFT(s3[p][i-s[p].low],sinusiods);
      };
   };
   a:=s3;
   proc 0 {
      filter(a);
      invert(a);
   };

   s:=a;
   par p from 0 to m - 1 {
      var i;
      for i from s[p].low to s[p].high {
         FFT(s[p][i-s[p].low],sinusiods);
      };
   };
   s2:=s;
   par p from 0 to m - 1 {
      var i;
      for i from s[p].low to s[p].high {
         FFT(s3[p][i-s[p].low],sinusiods);
      };
   };
   a:=s3;
   proc 0 {
      moveorigin(a);
      descale(a);
      writefile("newclown.ppm", a);
   };
};

function array[complex] computesin() {
   var elements:= n/2;
   var sinusoid:array[complex, elements];
   var j;
   for j from 0 to (n / 2) - 1 {
      var topass:Float;
      topass:=((2 * pi() * j) / n);
      sinusoid[j].i:=-sin(topass);
      sinusoid[j].r:=cos(topass);
   };
   return sinusoid;
};

function Int getLogn() {
   var logn:=0;
   var nx:=n;
   nx := nx >> 1;
   while (nx >0) {
      logn++;
      nx := nx >> 1;
   };
   return logn;
};

function void moveorigin(var data: array[complex,n,n]) {
   var i;
   for i from 0 to n - 1 {
      var j;
      for j from 0 to n - 1 {
         data[i][j].r:=data[i][j].r * pow(-1,(i + j));
         data[i][j].i:=data[i][j].i * pow(-1,(i + j));
       };
   };
};

function void descale(var data: array[complex,n,n]) {
   var i;
   for i from 0 to n - 1 {
      var j;
      for j from 0 to n - 1 {
         data[i][j].r:=data[i][j].r / (n * n) ;	
         data[i][j].i:=-(data[i][j].i / (n * n));
      };
   };
};

function void invert(var data : array[complex,n,n]) {
   var i;
   for i from 0 to n - 1 {
      var j;
      for j from 0 to n - 1 {
         data[i][j].i:=-data[i][j].i;
      };
   };
};

function void FFT(var data : array[complex,n], var sinusoid:array[complex]) {
   var i2:=getLogn();
   bitreverse(data); // data decomposition
   var f0:Double;
   var f1:Double;
   var increvec;
   for increvec from 2 to n {
      i2:=i2 - 1;
      var i0;
      for i0 from 0 to ((increvec / 2) - 1)  {
         // below computes the sinusoid for this spectra
         var i1;
         for i1 from 0 to n - 1 {
            // do butterfly for each point in the spectra           
            f0:=(data[i0 + i1 + (increvec / 2)].r * sinusoid[i0 << i2].r)- (data[i0 + i1 + (increvec / 2)].i * sinusoid[i0 << i2].i);           
            f1:=(data[i0 + i1 + (increvec / 2)].r * sinusoid[i0 << i2].i)+ (data[i0 + i1 + (increvec / 2)].i * sinusoid[i0 << i2].r);
		   
            data[i0 + i1 + (increvec / 2)].r:= data[i0 + i1].r- f0;
            data[i0 + i1 + (increvec / 2)].i:=data[i0 + i1].i - f1;
            data[i0 + i1].r := data[i0 + i1].r + f0;
            data[i0 + i1].i := data[i0 + i1].i + f1;

            i1:=(i1 + increvec) - 1;
         };
      };
      increvec:=(increvec * 2) - 1;
   };
};

function void loadfile(var name:String,var data:array[complex,n,n]) {
   var file:=open(name,"r");
   readline(file);
   readline(file);
   readline(file);
   readline(file);
   var i;
   for i from 0 to n - 1 {
      var j;
      for j from 0 to n - 1 {
         var red:=readchar(file);
         readchar(file);readchar(file);
         data[i][j].r:=red;
         data[i][j].i:=red;
       };
   };
   close(file);
};

function void writefile(var thename:String, var data:array[complex,n,n]) {
   var file:=open(thename,"w");
   writestring(file,"P6\n# CREATOR: LOGS Program\n");
   writestring(file,itostring(n));
   writestring(file," ");
   writestring(file,itostring(n));
   writestring(file,"\n255\n");
   var i;
   for i from 0 to n - 1 {
      var j;
      for j from 0 to n - 1 {
         writebinary(file,data[i][j].r);
         writebinary(file,data[i][j].r);
         writebinary(file,data[i][j].r);
      };
   };
   close(file);
};

function Int lowpass(var i:Int, var j:Int) {
   var val:=sqr(i) + sqr(j);
   if (sqrt(val) < filterThreshold) return 1;
   return 0;
};

function Int highpass(var i:Int, var j:Int) {
   var val:=sqr(i) + sqr(j);
   if (sqrt(val) > (255-filterThreshold)) return 1;
   return 0;
};

function void filter(var data: array[complex,n,n]) {
   var i;
   for i from 0 to n - 1 {
      var j;
      for j from 0 to n - 1 {
         data[i][j].r:=data[i][j].r * lowpass(i,j) * highpass(i,j);
         data[i][j].i:=data[i][j].i * lowpass(i,j) * highpass(i,j);
      };
   };
};

function void bitreverse(var a:array[complex,n]) {
   var j:=0;
   var k:Int;
   var i;
   for i from 0 to n-2 {
      if (i < j) {
         var swap_temp:Double;
         swap_temp:=a[j].r;
         a[j].r:=a[i].r;
         a[i].r:=swap_temp;
         swap_temp:=a[j].i;
         a[j].i:=a[i].i;
         a[i].i:=swap_temp;
      };
      k := n >> 1;
      while (k <= j) {
         j := j - k; 
         k := k >>1;
      };
      j := j + k;
   };
};

This version requires at least Mesham version 1.0

Notes

The algorithm is relatively simple, one drawback is that, even though the transpositions are distributed, after the first 2d FFT all the data must be sent back to process 0 for filtering, and then the data is redistributed. It would improve runtime if we could filter the data without having to collect it all on a central one - this would be an interesting improvement to make to the algorithm.

Note: This example will produce an image in the Portable PixMap format (PPM), viewers of these on Unix based systems are easy to come by (i.e. eye of gnome) but on Windows are slightly more difficult. Windows users might want to rewrite some of the last bit on process 0 so that a BitMaP is created.

Download

You can download the entire Image processing package here there is also a legacy version for Mesham 0.5 here

There is also a simplified FFT code available here which the imaging processing was based upon and a version which can be run with any number of processes decided at runtime here.